中国研究生创“芯”大赛由教育部学位管理与研究生教育司指导，中国学位与研究生教育学会、中国科协青少年科技中心主办，清华海峡研究院作为秘书处。赛事作为中国研究生创新实践系列赛事之一，是面向全国高等院校在读研究生的一项团体性集成电路设计创意实践活动，为参赛学生提供知识交流和实践探索的宝贵机会，至今已成功举办四届。

Cadence 连续五年全力支持中国研究生创“芯”大赛，在去年首次设计了一道关于 3DIC 互联优化算法的企业命题后，今年延续去年的出题方向，期待吸引更多队伍参与进来，让我们在这个前沿技术领域与高校有更多的交流与合作机会。

为进一步服务国家集成电路产业发展战略实施，Cadence 将大学计划作为公司在中国发展的一项长期战略，并提供了专业的技术团队和雄厚的研发实力作为坚强的后盾。Cadence 在致力于推动与成就中国商业客户成功的同时，也专注于促进中国集成电路及系统设计领域优秀人才的培养。

大赛重要时间点

报名启动时间：2022年4月1日

Cadence 企业命题专场宣讲: 2022年4月10日14：00

报名截止时间：2022年6月20日

初赛作品提交截止时间：2022年6月24日

决赛时间：2022年7月29日-8月1日

Cadence 专项奖设置

• 一等奖一队，奖金 10,000 元
• 二等奖三队，奖金 5,000 元

Cadence 企业命题专场宣讲

为了参赛者能够更好理解 Cadence 的企业命题，Cadence 资深芯片专家邓力群将于 2022 年 4 月 10 日下午 14：00 进行中国研究生创"芯"大赛 —— Cadence 企业命题专场宣讲！

宣讲地址

您可扫描下方二维码：

讲师简介

邓立群

邓立群，Cadence 公司数字集成电路自动化设计研发中心产品工程总监，主要负责数字后端平台的布局布线、PPA 优化、先进工艺支持以及三维集成电路等 EDA 工具设计和技术支持。

附件下载

扫码添加大赛秘书处微信加入赛题交流群，获取赛题附件。

Cadence 赛题

三维集成电路的多层模块划分最优化算法

赛题背景

一个数字电路的 Verilog 网表通常由多个模块（module）组成。模块内部的逻辑单元、寄存器之间有大量连接。模块和模块之间也互相有信号的连接。当设计者在早期规划芯片的布图结构 (Floorplan）阶段，通常可先忽略模块内部连接，而更关注模块之间的连接关系。这样可以在不损失太多精度的同时，更快速地评估架构的可行性。

同时我们也需要考虑各个模块的面积（通常由该模块内部 instance 的总面积决定），使得这些模块在后端实现的布局布线阶段，能够在芯片的版图上得到合理的面积分配。

此处为了简化问题的形式，我们暂时忽略整个芯片对外的输入输出（I/O) 而只考虑模块之间的连接。

例如，图1是拥有7个模块（Verilog module，非hard IP block）的一个芯片。模块有不同大小的面积。模块之间的连接用线段表示，线段上的数字代表了连接的信号个数。

图1：模块大小和连接关系的例子

三维集成电路与模块划分

用三维集成电路来实现一个芯片，会遇到的一个常见问题是：如何对整个芯片的电路模块进行划分，使这些模块被分配到多个裸片（Die）上。

图2是一个把电路划分成两部分，并分配到上下两个同样面积的裸片上的例子。划分之后，两部分电路之间的连接，通过裸片之间的堆叠工艺实现，比如常见的有 Bump 以及 TSV（Through Silicon Via）

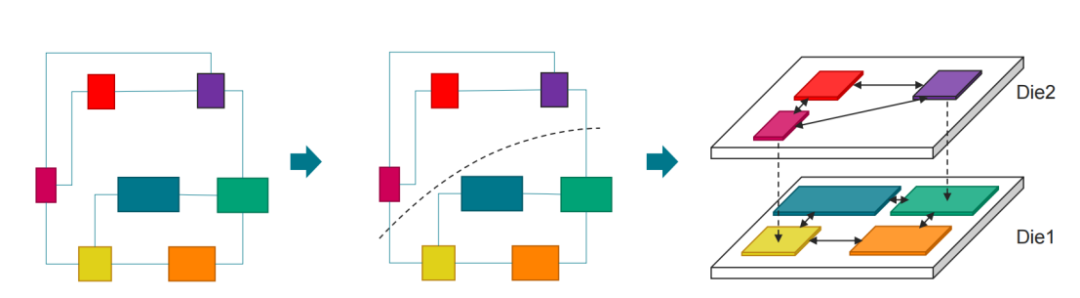
图2：划分到两个裸片的例子

关于TSV

TSV 提供了信号穿越裸片衬底的通路。但是它自身也需要占据一部分面积，因此也必须考虑到 TSV 带来的额外的面积需求。

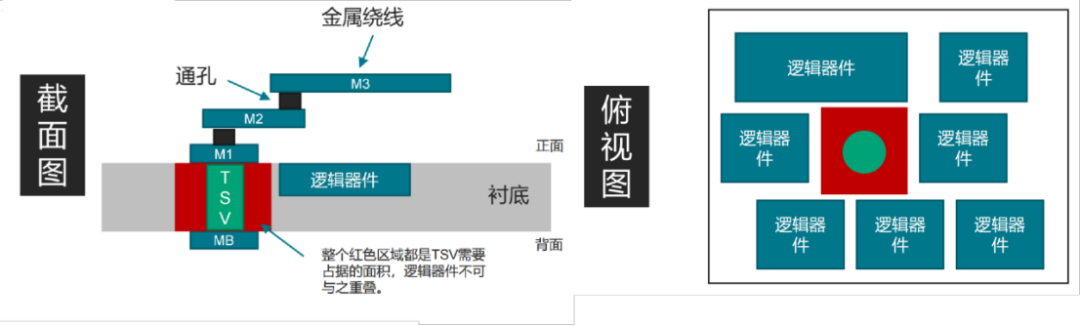
图3：TSV 示例

当多层裸片堆叠时，凡裸片和裸片界面处穿过衬底的地方需要 TSV。

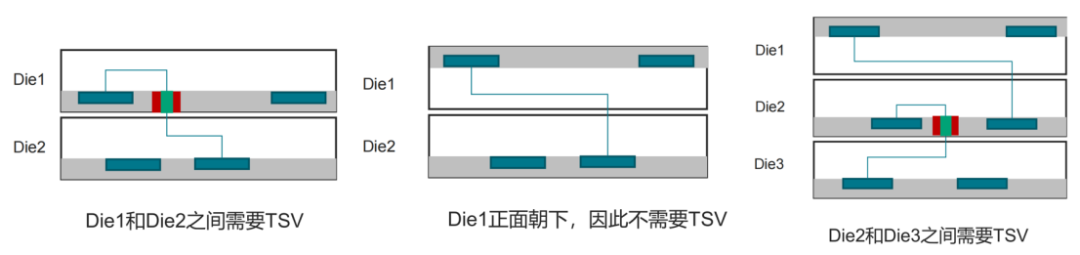
图4：多层裸片间的 TSV

关于Feedthrough

当多层裸片堆叠时，比方说三层：从第一层到第三层的信号连接，即使在逻辑上并没有和第二层的模块有任何关系，物理上也必须穿过第二层，即 Feedthrough。从而有可能会产生额外的 TSV。

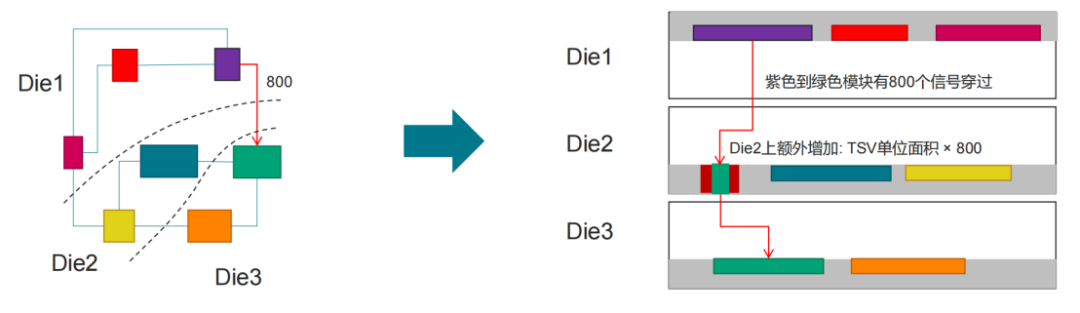
图5：Feedthrough

约束条件

三维划分需要考虑的硬性约束条件有：

1 ► 一个裸片上所有模块的总面积，加上这个裸片上所需的 TSV 的总面积，不能超过裸片的面积，即面积利用率不能超过100%。

2 ► 相邻两个裸片的界面上，可容纳的 Bump / TSV 的数量是有上限的。

约束条件的例子

图 6 是面积约束条件的一个例子（假设每根线代表100个信号）。如果不考虑面积，左边的划分是最好的，因为只需要 200个 bump。但是第一层的模块总面积已经超过了裸片面积。

此时采用右边的方案，bump 数量增加到了 500个，但只要仍然小于两个 die 之间所能容纳 bump 数量的上限，同时模块总面积也并没有超过裸片面积，则仍然是可行的。

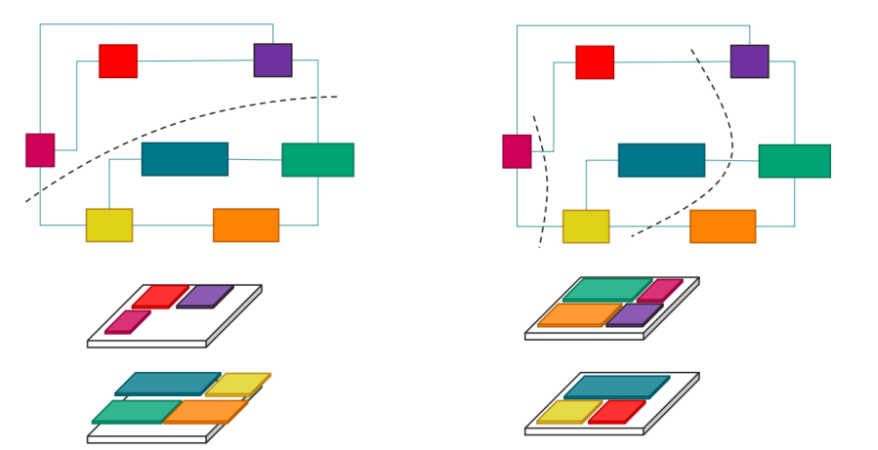
图6：面积约束条件的例子

题目要求

对于主办方给定的：

• 模块连接图（包含模块面积以及连接关系和信号数量）
• 裸片尺寸、TSV 单位尺寸
• 相邻两个 Die 之间的 Bump / TSV 数量上限（为简化题目，假设 Bump 和 TSV 的数量上限相同）

要求把所有模块划分到 3个裸片上。不考虑整个芯片对外的 I/O。堆叠方向如图 7 所示，灰色表示衬底：

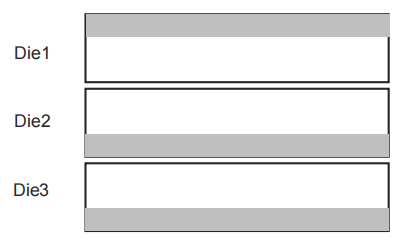
图7：堆叠方向

在满足硬性约束条件下，最优化以下两个目标：

1. 三个裸片上模块的面积利用率尽可能相同。避免出现有些裸片过于拥挤而有些裸片大片空白的情况。利用率=（模块总面积 + TSV 总面积）÷ 裸片面积
2. 裸片间 bump / TSV 数量尽可能少。

附加题 - 考虑模块布局与总线长

基本题并不考虑模块在版图上的具体位置，只计算其面积和连接数。附加题要求提出一种算法并尝试实现：在考虑模块布局（无缝铺满整个裸片区域，形状可以是矩形或直角多边形，如图 8 所示）的前提下，使总线长最短。

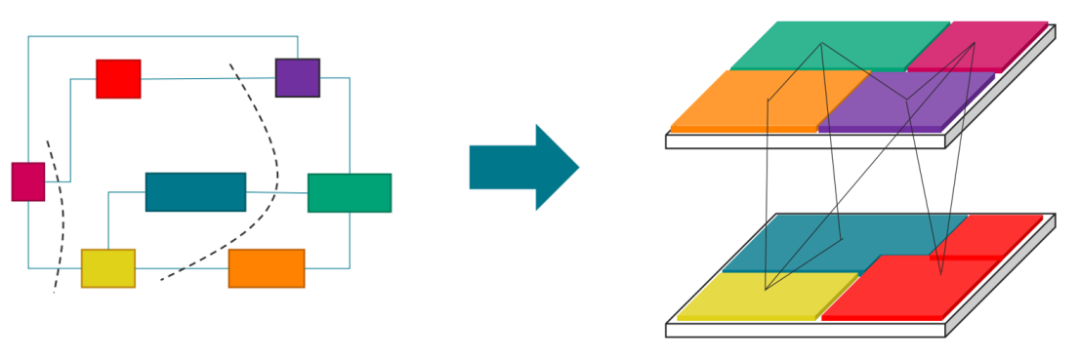
图8：模块布局与总线长

注1：由于利用率总是小于 100%，因此铺满后每个模块的占地面积将大于它的初始面积。但不可小于初始面积。注2：总线长的计算用模块几何中心之间的水平距离来简化。注3：TSV 假设均布在裸片上，可先不考虑其具体位置，但面积需算入。

提交要求

1. PPT报告
2. 优化算法代码
3. 可重现的计算结果

（文章来源公众号： Cadence楷登）